Topic Modelling : Latent Dirichlet Allocation, an introduction

Published by

Rishu Shrivastava

on

June 11, 2020

Imagine finding meaning out of a news content which you haven’t seen before. Topic Modelling is a type of statistical modelling that solves the purpose of finding abstract topics from a corpus of documents. Topic modelling provides methods for searching, organising and summarising large volumes of data. This modelling technique is primarily used in cases where you are trying to recommend shopping items or cluster emails or set of images into categories.

In this blog, I will try to cover one of the topic modelling technique called Latent Dirichlet Allocation or LDA (in short) on a BBC News dataset along with providing intuition and code using Scikit-learn.

Latent Dirichlet Allocation

Latent Dirichlet Allocation is a generative probabilistic model for collection of discrete data such as text corpora. LDA is a three-level hierarchical Bayesian model, in which each item of a collection is modeled as a finite mixture over an underlying set of topics. Each topic is, in turn, modeled as an infinite mixture over an underlying set of topic probabilities.
Introduction from Original Paper by David M. Blei; Andrew Y. Ng; Michael I. Jordan (2003) [Link]

Fig 0: Overall view of LDA + Topic Modelling

Intuition

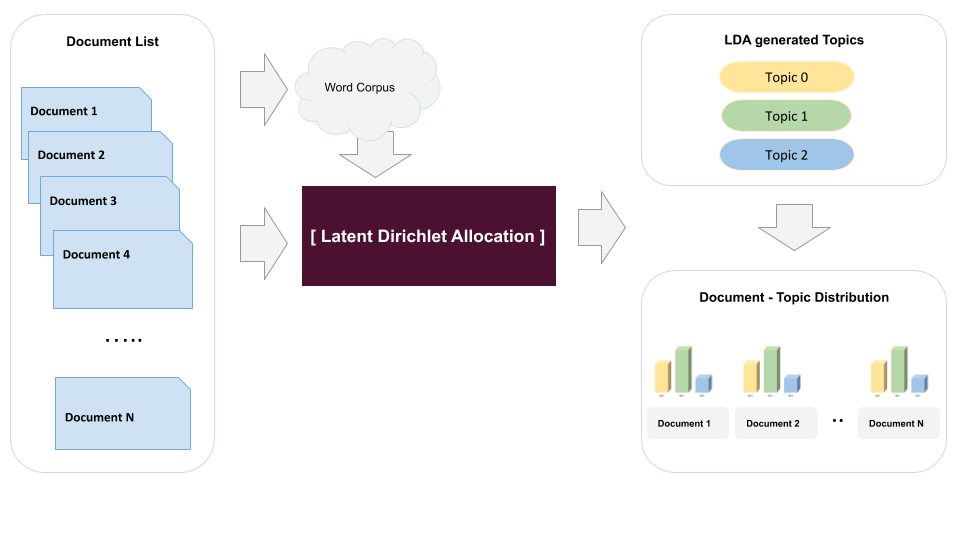
Let’s assume you have list of 1000 documents and each document has around 1000 words in them. If we take all of the words from all of 1000 documents and map them to every document in the list, we could find a pattern where some documents would map to similar set of words. Hence we could generate a cluster from the similar words. But this approach is computationally expensive since you will have to iterate over 1000×1000 times for finding pattern.

Now, with the above scenario, let us introduce a hidden layer between the documents and the words it contains. Let us now assume we have 3 topics that could possibly be created from document list. These 3 topics are some random topics which are not observed i.e. we have no idea of the existence of any such topic before hand in the documents.

Fig 1 : Document – Topic – Word Mapping using LDA

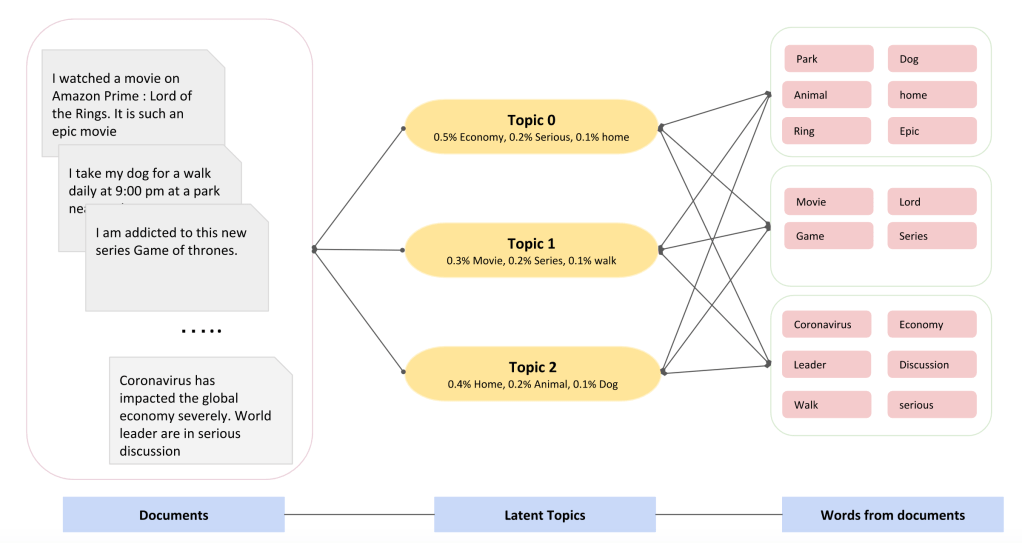
Let us now map each of the words in the document to a particular topic. With this approach we map the words to random topics and documents to each of the topics. This helped us in reducing the iteration to 1000×3 (words to topics) + 3×1000 (topics to documents) from the initial iteration. Every topic that is being represented is rather a probability percentage of distribution of words as in the fig.

Latent Dirichlet Allocation uses the above intuition to determine cluster out of collection of words in a document. The above model gives a trim-down version of a model.

Mathematical Model

I will try to briefly cover the mathematical model of the LDA that was originally provided in the paper.

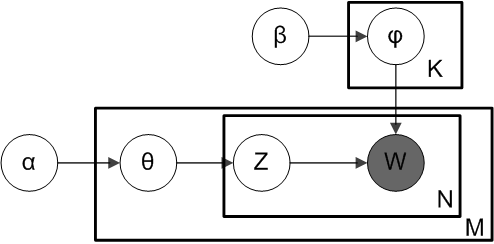
Fig 2: Latent Dirichlet Allocation Model – Plate Notation – Reference Link

Assumptions

We assume the data to be a list of documents M1,M2,M3,.. Mn
Every document is a collection of words without the stop-words.
Relationship between two words is not considered in the model.
We want K topics from the list of words in a document.

Parameters

M denotes the number of documents
N is number of words in a given document (document i has $N_{i}$ words)
α is the parameter of the Dirichlet prior on the per-document topic distributions
β is the parameter of the Dirichlet prior on the per-topic word distribution
$\theta _{i}$ is the topic distribution for document
i $\varphi _{k}$ is the word distribution for topic
k $z_{ij}$ is the topic for the j-th word in document
i $w_{ij}$ is the specific word.

Using the above model our goal is to infer the probability distribution of the words in a hidden topic. The variable W is grey out which means it is an observable variable and other hidden. As proposed in the original paper, a sparse Dirichlet prior can be used to model the topic-word distribution, following the intuition that the probability distribution over words in a topic is skewed, so that only a small set of words have high probability.

Code Walk

All the codes are available in a Jupyter notebook. In this section, I will briefly touch on the main points of the code and steps followed on implementing LDA on a BBC News dataset.